- Below I will use colors to represent Jordan canonical forms.
- Let $T$ be an operator on an $n$-dimensional complex vector space. Suppose that $T$ has $k$ distinct eigenvalues $\lambda_1, \ldots, \lambda_k$. For each eigenvalue $\lambda_j$ of $T$ there corresponds a unique positive number $m_j$ and a unique nonincreasing $m_j$-tuple $\bigl(q_{j,1},\ldots,q_{j,m_j}\bigr)$ of positive integers such that there exists a basis of the null space of $(T- \lambda_j I)^n$ which consists of $m_j$ Jordan chains (of $T$ corresponding to $\lambda_j$) of lengths $q_{j,1},\ldots,q_{j,m_j}$.
- The distinct eigenvalues $\lambda_j$, $j \in \{1,\ldots,k\}$ together with the corresponding $m_j$-tuples $\bigl(q_{j,1},\ldots,q_{j,m_j}\bigr)$, determine the Jordan canonical form of the operator $T$.
- In the figures below I represent a Jordan canonical form using colored squares instead on numbers. White squares stand for $0$s, black squares stand for $1$s, and the squares of various colors represent distinct eigenvalues.
| 4 distinct eigenvalues with lengths of Jordan chains 
|
3 distinct eigenvalues with lengths of Jordan chains 
|
|
6 distinct eigenvalues with lengths of Jordan chains 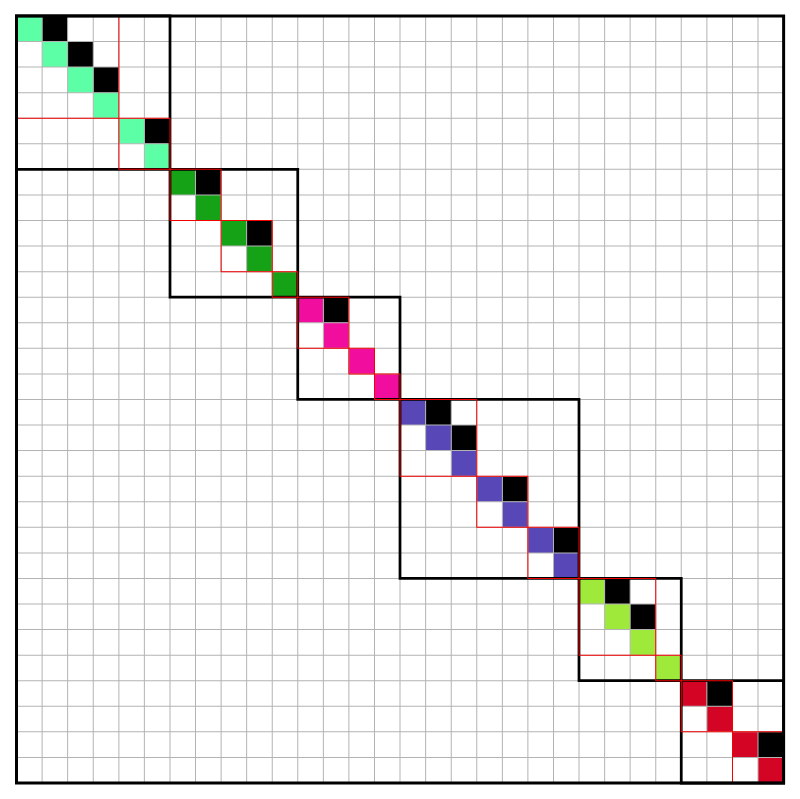
|
3 distinct eigenvalues with lengths of Jordan chains 
|
-
I wrote Mathematica program to generate random Jordan normal forms with small number of eigenvalues and short Jordan chains. Below are few colored Jordan normal forms generated by Mathematica. In some pictures I emphasized the distinct eigenvalues (with black framed blocks) and their Jordan chains (with red framed blocks).
Click on icons for bigger images.



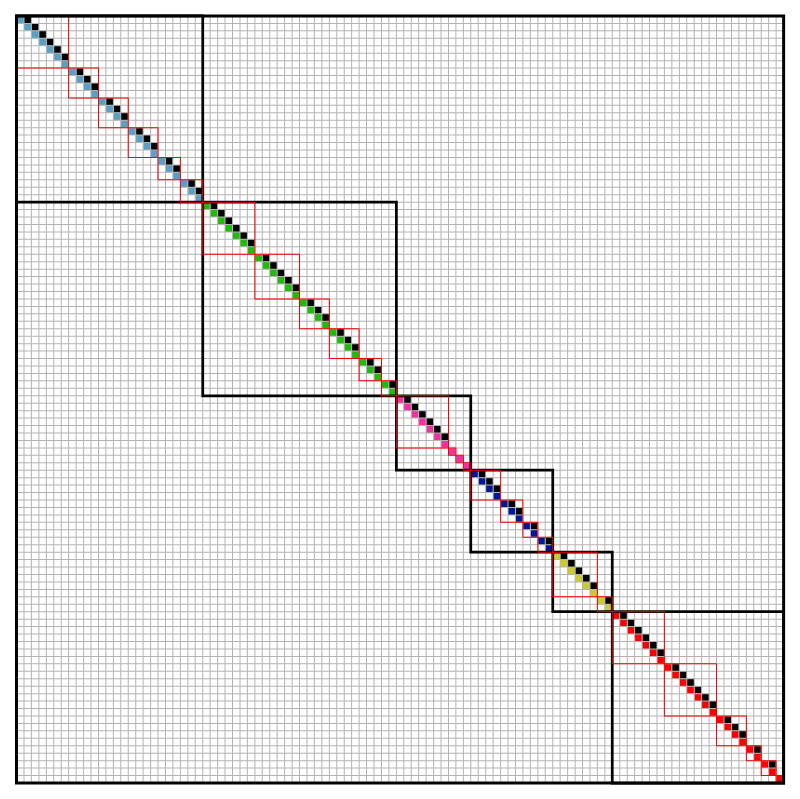
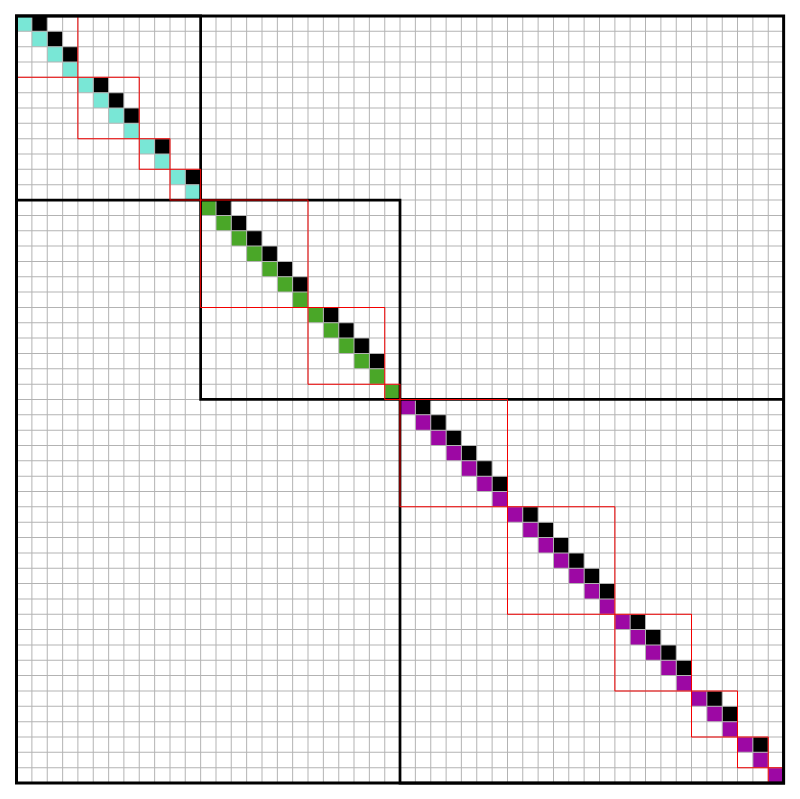



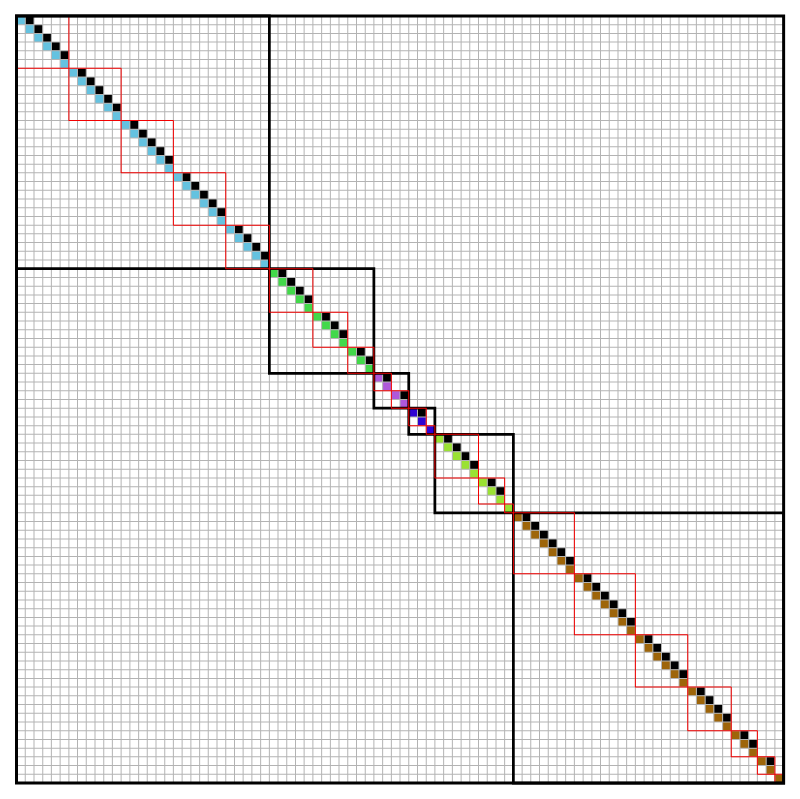






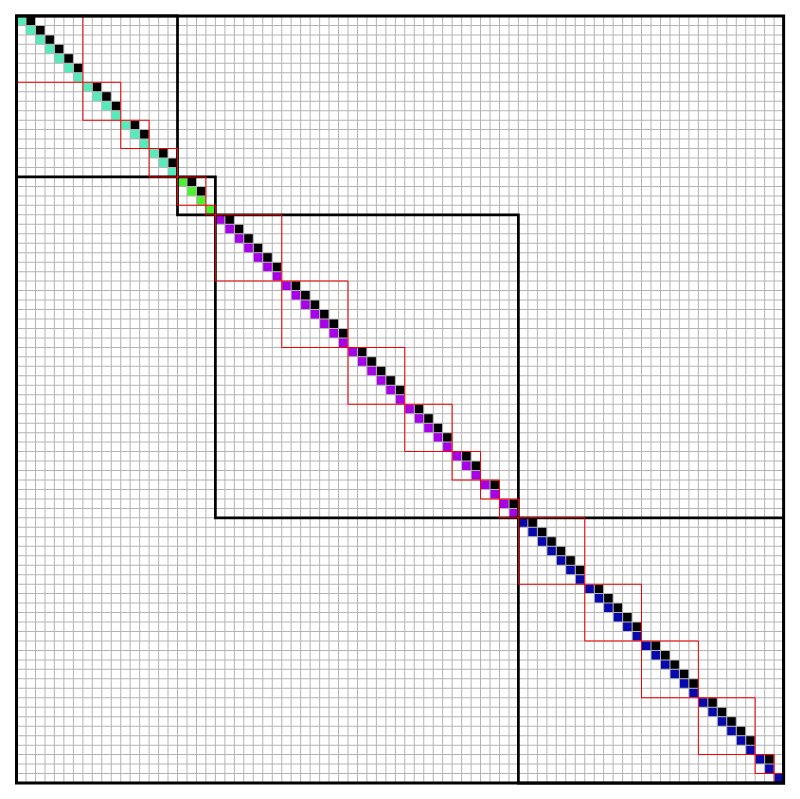

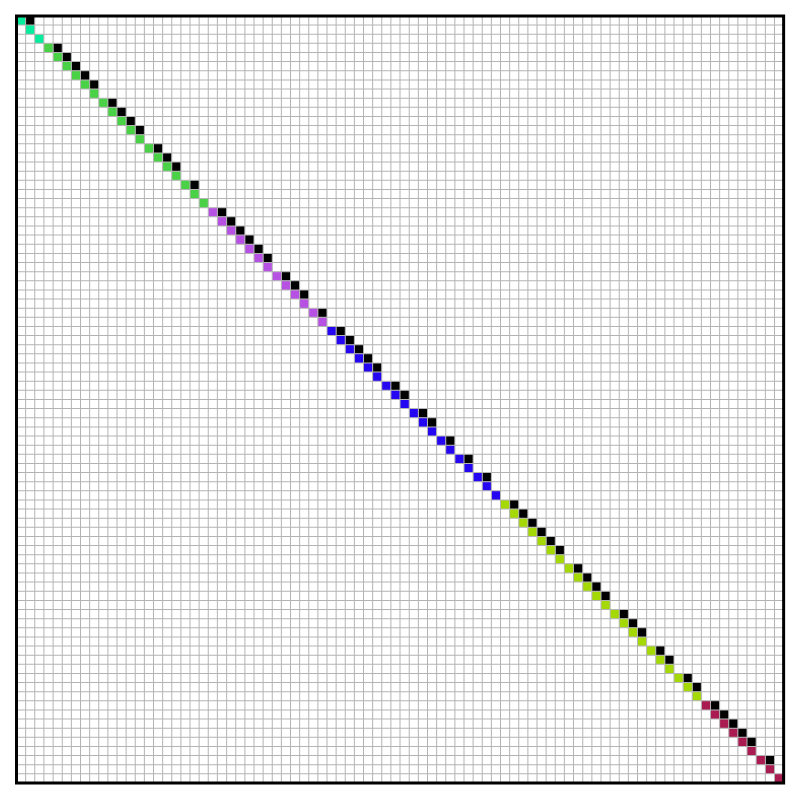














- Looking at a picture of a Jordan normal form you can contemplate the following questions about a corresponding operator: How many distinct eigenvalues does this operator have? What are the dimensions of the corresponding eigenspaces? What are the dimensions of the corresponding generalized eigenspaces? How many Jordan chains correspond to each eigenvalue and what are their lengths? If I square this operator, how would the Jordan normal form of that operator look like?
- Here is the the first version of my notes on the Jordan normal form of a matrix representation of a linear operator.
- Updated version of Inner Product Spaces notes. Please read carefully and report errors, since I changed notation several times, so there might be some unrelated symbols in floating around.
- Updated version of Inner Product Spaces notes.
- Updated version of Inner Product Spaces notes.
- Here is the beginning of my notes on Inner Product Spaces.
- Some of the material that relates to nonneqative inner product spaces (that is to nonnegative hermitian sesquilinear forms) is on this web page.
- My notes on Eigenvalues and Eigenvectors of linear operators on complex finite dimensional vector spaces.
- I modified my notes on Linear operators by adding the proof that I did in class today.
- As I emailed you earlier, we will have "in class" exams on Wednesday, February 4 and Wednesday, March 4. The exams will start at 11am and last until 1pm for students who started at 11am. For students who are not able to start at 11am, the exam will start at noon and last until 2pm. Both exams will be held in BH 403.
- The second part of Assignment 1 is due on Friday, February 6.
-
Problem 4. Let $D$ be a finite set and let $\mathbb F$ be a scalar field. Then the set of all functions defined on $D$ with values in $\mathbb F$ is a vector space over $\mathbb F$ with the addition and scalar multiplication of functions defined pointwise. This space is denoted by ${\mathbb F}^D$.
-
(a) Prove that ${\mathbb F}^D$ is finite dimensional if and only if $D$ is finite. (b) If $D$ is finite, then $\dim \bigl({\mathbb F}^D\bigr) = |D|$.
-
-
Problem 5.
Let $\mathcal V$ be a vector space over $\mathbb F$. Let $\mathcal A$ be a linearly independent subset of $\mathcal V$. Let $u \in \mathcal V$ be arbitrary. By $u + \mathcal A$ we denote the set of vectors $\{u+v : v \in \mathcal A \}$.
-
(a) Prove the following implication. If $w \notin {\rm span}\, \mathcal A$, then $ w + \mathcal A$ is a linearly independent set. (b) Is the converse of the implication in (a) true? (c) Let $\alpha_1,\cdots,\alpha_n \in \mathbb F$, let $v_1,\ldots, v_n$ be distinct vectors in $\mathcal A$ and let $w = \alpha_1 v_1 + \cdots + \alpha_n v_n$. Find a necessary and sufficient condition (in terms of $\alpha_1, \ldots, \alpha_n$) for the linear independence of the vectors $v_1 + w, \ldots, v_n + w$.
-
- Problem 6. Let $\mathcal V$ be a vector space over $\mathbb F$ and $T \in {\mathcal L}(\mathcal V)$. Assume that there exists a function $f: \mathcal V \rightarrow \mathbb F$ such that $Tv = f(v)\, v$ for each $v \in \mathcal V$. Prove that $T$ is a multiple of the identity mapping. That is, there exists $\alpha \in \mathbb F$ such that $Tv = \alpha\, v$ for each $v \in \mathcal V$. (A plain English explanation: The equation $Tv = f(v)\, v$ is telling us that $T$ scales each vector in $\mathcal V$ by the scaling coefficient $f(v)$. The point of the problem is to prove that $T$ must scale each vector by the same coefficient. This is a consequence of the linearity of $T$.)
- On Monday we will start our new topic: Linear operators. Here are my notes on the topic.
- Today I wanted to demonstrate a Mathematica notebook which shows that the complicated trigonometric identity used by 6 students to solve Problem 1 from Assignment 1 is wrong. Instead of demonstrating that notebook in class, I am posting it. Open this notebook is Mathematica v8.
- On Friday I used Mathematica to illustrate functions from the space ${\mathcal S}_1$ from Problem 1 on the Assignment. Here is the Mathematica file that I used.
-
To play with the above file in Mathematica, right-click on the underlined word "Here"; in the pop-up menu that appears, your browser will offer you to save the file in your directory. Make sure that you save it with the exactly same name "Spaces_S_gamma_v8.nb". Notice that I use the underscore to separate words in the file name. After saving the file you can open it with Mathematica_v8. You need to find a campus computer with Mathematica_v8 installed on it (for example BH 209, BH 215). You will find Mathematica as follows (this sequence might differ on different campus computers)
Start -> Programs -> Math Applications -> Mathematica. Open Mathematica first, then open Spaces_S_gamma_v8.nb from Mathematica. You can execute the entire file by the following manu sequence (in Mathematica):Evaluation -> Evaluate Notebook. - More information on how to use Mathematica you can find on my Mathematica page.
- If you have problems running files that I post, please let me know. If you spend some time learning how to use Mathematica you will enhance your understanding of math that you are studying.
- Samantha Smith pointed out to me that statement (c) in Problem 7.2 in the notes Vector Spaces was wrong. I restated Problem 7.2 in the new version of the notes Vector Spaces. Now I am asking you to figure out what was wrong before.
- I reformulated few statement in the new version of the notes on Bases.
- It is not required, but it is strongly encouraged that you write your assignment in LaTeX. A paper printout is still preferred for grading.
- LaTeX is a document preparation system which is widely used by mathematicians. In fact it is the standard for professional mathematical publications. It is completely free. I encourage you to learn LaTeX while you are here at WWU. There are lots of students and faculty members who are expert users. You can get a lot of help to get started.
-
There is an abundance of information about LaTeX on the web. Here are a few sites to start with.
- Introduction from LaTeX project site.
- LaTeX for Complete Novices by Nicola L. C. Talbot.
- LaTeX help from NASA.
- A LaTeX introduction from Tobias Oetiker site (a pdf file).
- Here is the LaTeX file that I used to produce Bases2013.pdf. Right-click on the underlined word "Here"; in the pop-up menu that appears, your browser will offer you to save the file in your directory. Make sure that you save it with the exactly same name, Bases2013.TeX.
- If you have a problem with any aspect of LaTeX ask me or any LaTeX enthusiast at WWU. LaTeX community is very willing to help you to discover this amazing tool. Also, keep on googleing and you will find a site that will answer your question.
- My notes of Chapter 1; the title of the notes is Vector spaces.
- My notes of Chapter 2; the title of the notes is Bases.
-
The first three problems for Assignment 1 are as follows: (Notice that the numbers are different from what I stated in class.)
- Problem 1. Problem 7.1 in my notes on Chapter 1 (Vector spaces) The easiest way to do this problem is to represent each $\mathcal S_\gamma$ as a span. Your proof could start as follows: I claim that $\mathcal S_\gamma = {\rm span}\bigl\{ \ldots \bigr\}$. Here is a proof of my claim. (Write your proof.)
- Problem 2. Problem 7.2 in my notes on Chapter 1 (Vector spaces)
- Problem 3. Problem 7.5 in my notes on Chapter 1 (Vector spaces) Before doing this problem solve Problem 7.3 and internalize my solution of Problem 7.4.
- The information sheet
- Chapter 1
- Chapter 2
- Some relevant Wikipedia links: